Keywords: structured surfaces three-dimension structures grooves transversal lateral periodic displacement wave flow drag reduction turbulent
From conventional 2D to 3D structures and from RANS to LES codes
Whilst the benefit of structured surfaces has been known for long, it has mostly been addressed till now to two dimension structures with flow drag reduction limited to 10-12% (see site web section_ Structured Surface 2D). The objective of the present study is to analyse the benefits of more complex structure shapes. Performance of structured surfaces may be analysed in using Computational Fluid Dynamic codes (previous section) ranging from the Direct Numerical simulation (DNS – Full turbulence simulation) to the Reynolds Average Navier Stokes (RANS – Full turbulence modelling). These codes are used for very different purposes. Concerning the first code, it is used for an in depth flow mechanism analysis at the expense of a high computation cost and, concerning the second code, it is used for engineering studies. The Large Eddy Simulation code (LES – Partial simulation and partial modelling of turbulence), intermediate in its features between the two codes, tends to be used more often for engineering applications. It seems to be a good compromise for the study of complex boundary flows.
Flow simulations with RANS and LES codes
A RANS code has been successfully used for the study of two dimension (2D) structures providing some means for analysing 2D structures in terms of flow drag reduction and secondary flows around these structures. However, when tested in a more complex boundary flow situation (typically, the case of an oscillating plate), the RANS code failed. As a consequence, LES has been tested for the steady of more complex boundary layers (oscillating plates and 3D structures).
A LES code has been successfully validated in the case of an oscillating plate (Section 2 below). This task was required prior to the study of complex structured shapes.
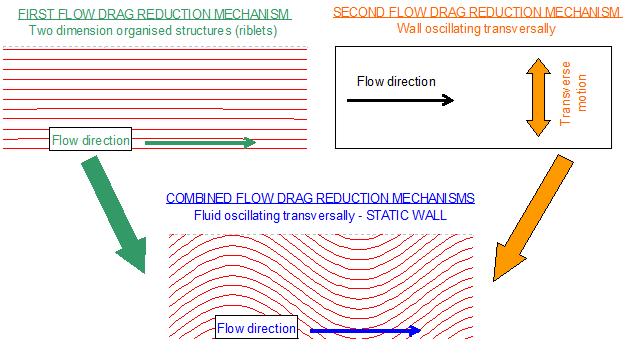
A LES code has then been used for the study of a specific three dimension (3D) structure (Section 3 below). This 3D structure combines the principle of two turbulence reduction mechanisms: a) 2D structure and b) transverse flow oscillation. These structures appear as sine waves mounted in direction of the main flow with hills and valleys sized similarly to 2D riblets. The amplitude and the period of the sine waves are sized similarly to a transverse oscillating flow (oscillating plate). A parametric study has been carried out in order to verify the effect of a change in both oscillation amplitude and period.
Similitude laws are provided in this report for transposing the results from the present study (Re Nb=14 000) to considerably larger Reynolds numbers (gas transport – 107<Re<108). In particular, the 2D structures and sine wave parameters are roughly proportional to the pipe diameter / Reynolds nb ratio (D / Re).
_
Conclusion
A LES Code could establish the drag reduction provided by a plate oscillating transversely to the main flow direction. Maximum drag reduction is obtained for a dimensionless period of 100. In this case, the drag reduction varies considerably with the amplitude of the oscillation (disregarding the input energy brought to the plate).
Two dimension riblets of the knife blade type provides a maximum drag reduction of the order of 10 %. The same result was found with a RANS code (see corresponding Web site page) and a LES code (above section 3.1).
Three dimension structured surfaces combining the above two flow drag reduction mechanisms (2D riblets and transposed transverse flow oscillation) provide a drag reduction of the order of 20 %. The maximum drag reduction was achieved for a dimensionless period of 100 and a maximum angle of the transverse oscillation of the order of 10 degrees.
In the case of gas transport in a pipeline with inlet and outlet pressure varying in a large ratio, the following parameters would change very little: the Reynolds number, the 2D riblet sizes, the dimensionless period, the dimensionless amplitude and the maximum angle of the structure oscillation. Considering the shape of these 3D structures, they could be manufactured in using the same process as the one anticipated for the 2D riblets. See corresponding Web site page.